【论文阅读】ViT-Vision Transformer（简介+代码+面经）

上一篇论文已经对Transformer模型进行了比较详尽的介绍，之后在NLP领域又相当多的有名的工作出现，例如Bert、GPT等，但是在计算机视觉领域中，怎样合理地把图像数据输入Transformer结构中仍然是是一个未确定的问题。

在正式介绍论文内容之前，先来看一下视觉任务中使用Transformer模型的难点，Transformer可以实现高度并行的一个重要原因是多头自注意力机制将训练从RNN的串行变为并行，其中QKV的计算均通过矩阵乘法进行，底层GPU会进行相当多的优化，那么训练效率会进一步提升。

而视觉任务中，如果将图像中每个像素看作token，使用注意力机制学习所有像素之间的注意力，会受到显存容量的限制（例如一张128*128的图像，共有16,384个元素，那么两两计算全局注意力的话需要对16,384*16,384大小的矩阵进行乘法，在硬件上不可行。那么作者就尝试了对图像分块得到patch，看作token来计算全局注意力（例如 128*128图像，patch大小为16*16，共得到64个tokens，那么计算全局注意力时只需进行64*64的矩阵乘法）（另外这里的patch=16其实直接从论文标题中得到的）。

论文的亮点除了将Transformer应用到视觉任务之外，还给出了大规模数据的条件下视觉任务中不需要依赖卷积操作的结论，在几乎没有添加归纳偏置（先验知识）的情况下，只要有足够多的数据，Transformer就可以超越当前的CNN-based SOTA。

最开始读这篇文章时，有点一头雾水的感觉，尤其是相关工作的介绍中，在看了李沐老师的论文精度系列的视频之后，明白了视觉任务中使用Transformer的难点后才豁然开朗，非常建议读者去看看李沐老师的论文精度系列！

此外在这篇博客中，模型结构介绍之后、代码介绍之前，我会尝试列出一些算法岗面试中常出现的问题，希望可以加深对ViT模型的理解，下面就进入正文。

摘要

Transformer结构已经成为NLP领域中的标准模型，但其在视觉任务中的应用还未被完全探索。当时的视觉任务中，还是将注意力机制和CNN一起使用，或者只是将卷积网络中的某些组件进行替换，其主体结构没有改变。而在这篇论文中，作者展示了视觉任务中CNN不是必要的，直接将图像patch序列输入到原始的transformer中也可以在图像分类任务上表现得很好。作者在大量数据上预训练并且迁移到多个中等规模和小规模的图像识别任务中（包括ImageNet、CIFAR-10、VTAB等），ViT(Vision Transformer)可以比当年的基于CNN的SOTA更好，并且训练资源更少（注意只是相对…怀疑的读者可以查阅论文中的TPUv3-core-days指标，\^_\^）

引言

基于自监督的模型（尤其是Transformer）已经在NLP领域大放异彩，主要的应用是在大型语料库中预训练，然后在特定任务的小数据集上微调。Transformer的计算高效性（并行）和可扩展性（编码器块可以堆叠多次），使得训练大规模网络成为可能。并且随着模型和数据集的增长，当时还没有看到模型能力饱和。

但是在视觉任务中，CNN仍是主流，尽管受到NLP模型的启发，当时的工作也只局限于将CNN结构和自注意力结合起来，或者完全将卷积替换掉。后者理论上更高效（因为自注意力可以直接对图像中任意位置的数据建模，但是CNN中只有在模型高层才可以对远距离位置的数据建模），但是由于这些工作设计的是特定的注意力模式（因为最开始我们提到，将每个像素看作token计算注意力，显存无法支持，那么这些工作里使用的是局部自注意力），所以在硬件设备上的训练效率仍然受限，这就使得CNN-based网络仍然是当时的SOTA。

受到NLP领域中Transformer模型的启发，作者尝试尽可能做少的修改、直接在图像上应用标准Transformer。于是，作者将图像切分为多个patch并且进行线性embedding操作，再输入到Transformer中。图像中的每个块patch可以类比为NLP中的token。作者在图像分类任务上使用监督学习方法训练网络。（在后续实验中，作者也尝试了使用自监督学习方法训练网络，虽然当时的效果不如监督学习方法，但也为之后的MAE提供了思路）

实验中发现，在中等尺寸的数据集（例如ImageNet）上训练ViT时，效果不如同等规模的ResNet，作者解释这可能由于Transformer中缺少CNN中的一些归纳偏置（也就是先验知识，例如平移不变性、局部性）。而当模型在大规模数据集上训练时，实验发现大规模数据训练会优于归纳偏置，在预训练任务和少样本学习任务中都会取得更好的结果。

结论

作者探索了直接将Transformer应用到图像识别任务。和之前视觉任务中使用自注意力的方法不同，作者除了在对图像打patch时添加了一些归纳偏置之外，没有再引入额外的归纳偏置。相反，作者将图像理解为patches的序列，并且使用Transformer中的原始编码器处理。这个简单并且可扩展的思路在大数据集上预训练时效果特别好。在很多图像分类任务上，ViT均和当时的SOTA效果相当或者更优，同时预训练相对来说更便宜。

虽然在分类任务上表现较好，但仍有很多需要进一步探索的空间，例如应用于检测、分割等其他视觉任务中。另外也应该自监督预训练策略，作者通过初步实验验证了ViT进行自监督训练的潜力，但和监督方法相比仍有差距。未来对ViT的进一步扩展会带来性能上的提升。

方法

ViT尽可能和原始的Transformer结构保持相似，不做太多的修改。下面是模型的结构图。

ViT

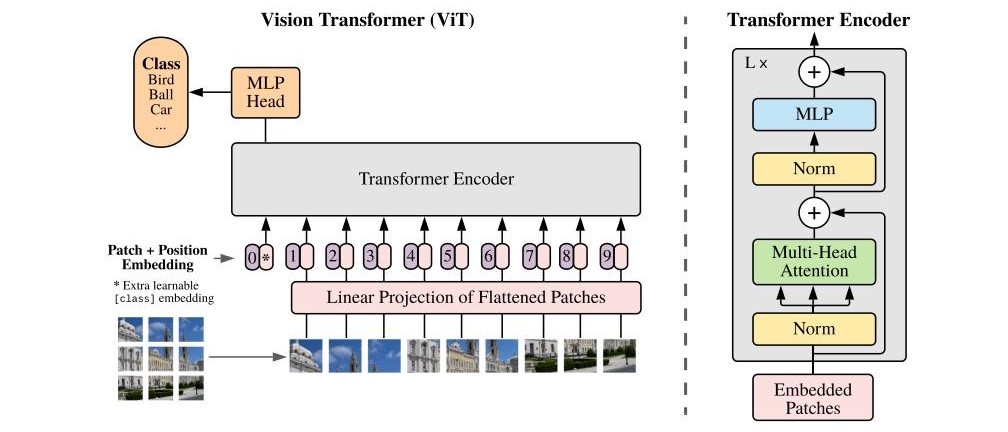
标准Transformer接收1D的token序列作为输入，为了处理2D图像，将图像切分为不同的小patch并展平(P为patch的尺寸)，那么其尺寸变化可见下，

\[\begin{equation} x\in R^{H*W*C} -> x\in R^{N*(P^2*C)} \end{equation}\]

由于模型中的潜向量尺寸为D，因此将patch展平并输入到线性投影层来映射到D维，得到的结果记作 patch embeddings。

ViT面向的是图像分类任务，那么自然想到在编码器之后添加一个分类头，分类头的输入可以是编码器的全部输出。但是为了和Bert中的处理比较相似，额外添加了一个可学习的 class token，与图像patch共同输入到编码器中，在前向计算的过程中 class token会融合所有patch的信息，代表从图像中提取的所有特征，然后作为分类头的输入。分类头在预训练时是单隐藏层的MLP，在微调阶段是单线性层。

接下来是位置编码，论文中使用标准的1D可学习位置编码（后续实验发现2D可学习的位置编码不会带来明显的效果提升），和原始的 patch embedding求和之后输入到编码器。

编码器完全遵循Transformer的设计，包括多头自注意力(Multiheaded self-attention, MSA)、MLP模块、层归一化、残差连接。MLP中使用GELU激活函数引入非线性计算。前向计算过程的第一步为每个图像patch经过线性映射层，与 class token拼接，再和位置编码进行element-wise加法。

\[\begin{equation} z_0=[x_{class};x_p^1E;x_p^2E;····;x_p^NE]+E_{pos},\qquad E\in R^{(P^2*C)*D},E_{pos} \in R^{(N+1)*D} \end{equation}\]

接着数据经过多个多头自注意力和残差连接。

\[\begin{equation} z'_l=Multihead\;SelfAttention(LN(z_{l-1}))+z_{l-1},\qquad l=1..L \end{equation}\]

然后经过带有残差连接的线性层。

\[\begin{equation} z_l=MLP(LN(z'_{l}))+z'_{l-1},\qquad l=1..L \end{equation}\]

最终经过多个编码层处理后，class token经过层归一化得到全局特征 y，作为分类头的输入。

\[y=LN(z_L^0)\]

和CNN相比，ViT中的归纳偏置（先验知识）更少。CNN中的卷积操作隐含了局部性、平移不变性等先验，而在ViT中只有对图像打patch和MLP中存在一些局部性和平移不变性，其余的关系（包括位置关系等）都需要模型从头学习。

另外作者提到了CNN和Transformer的一种混合结构模型——CNN提取的特征图展平，经过embedding和位置编码，输入到Transformer中。

作者的训练策略为：在大型数据集上预训练ViT，在下游任务上微调模型，微调时会删除预训练预测头，额外添加一个零初始化的前向层，得到下游任务类别的预测概率。有其他工作指出在微调阶段更适合使用高分辨率图像，如果这样做的话patch大小保持不变，那么就导致patch数量更多（序列长度更长）。Transformer的Encoder层输入输出尺寸保持一致，因此模型不必调整，但是预训练得到的位置编码不再适用。因此作者选择在预训练得到的位置编码中，根据其在原始图像中的位置进行2D插值（这种做法会向模型中添加一些先验知识）。

实验

作者通过丰富的实验验证了ViT在不同预训练数据规模、不同下游任务中的表现，并对比了CNN-based模型、混合模型的性能，最终的结论可以简述为以下几点：

使用中等规模数据预训练，ViT性能不如同等规模的CNN-based模型；
在大规模数据上进行预训练，在多个微调任务、少样本学习任务中，ViT可超越CNN-based模型，并且训练效率更高；
对ViT来说，除了编码层的堆叠数量之外，对图像设置的patch大小也会影响模型性能；
对模型中间得到的特征进行可视化发现，底层学习到的是一些纹理、边缘等低级特征；
对位置编码进行可视化发现，图像中相近patch、同行同列patch的注意力更高，这也和直觉一致；
对注意力距离（可理解为感受野）可视化发现，模型底层会同时关注到多种尺度的感受野（而CNN中只能学习到局部感受野的关系），而在模型高层主要是大的感受野，表明模型在学习全局注意力。

另外作者提到“Transformer的成功不仅是由于模型结构，也是因为自监督预训练的策略”，因此额外设计了一个自监督学习策略，参考NLP任务中的做法对图像中的部分patch进行mask掩码操作，通过图像重建来进行自监督学习预训练。实验表明和其他自监督学习方法相比，ViT效果更好，但是仍然不如监督学习预训练策略，未来仍值得关注和探索（MAE就做到了！！

以上就是ViT模型的设计思路，Transformer编码器完全延续了原始的设计，重点考虑了为图像打patch、为图像patch添加位置编码、添加 class token、分类头设计的问题，并且通过大量充分的对比实验描述了ViT的性能（建议读者可以看看原论文正文和附录中的实验，真的很全面，不愧是google…），至此NLP任务和CV任务实现了“大一统”，都可以使用相同的模型结构解决问题，直接推动了多模态领域的研究。另外作者对Transformer模型的理解也很前瞻，指出其有效性的原因不仅是并行的模型结构，也和自监督预训练策略有很大的关系，并通过比较简单的自监督学习验证了ViT的潜力，鼓励了未来对视觉检测、分割任务的研究。

面试常见问题

ViT将图像分割为固定大小的patch后，如何将这些patch转换为适合Transformer处理的序列？能否详细描述预处理流程中的关键步骤？

对patch进行线性embedding，维度变成模型hidden dims，并且与1D可学习的位置编码直接相加（element-wise add）。

预处理过程中要考虑恰当的patch大小，经过embedding之后，为了和NLP中的架构尽可能相似，会额外添加一个 class token与 patch embeddings进行拼接，最后和1D可学习的位置编码参数直接相加作为编码层的输入。

ViT的位置编码与传统NLP中的位置编码有何不同？如果不使用位置编码，会对模型性能产生什么影响？

Transformer中使用的位置编码是根据位置信息计算正余弦值，而ViT中选择1D位置编码参数，是可学习的；论文中对不使用位置编码的情况进行了对比实验，会导致模型性能稍有下降（大约下降3个百分点）。

ViT的”分类token”（class token）在模型中的作用是什么？为什么需要将它添加到patch序列中？

分类token在前向计算过程中会融合图像的全局信息，最终作为图像特征输入到分类头中，完成分类任务。

原论文中提到为了和NLP（BERT模型）中的设置尽可能相似，将其与patches进行拼接，作为编码器的输入，不过实验证明，如果不使用 class tokrn、而是为分类头输入编码器的输出，也可得到相近的性能。

ViT与CNN的核心区别是什么？为什么ViT在大规模数据集上表现更好，但在小数据集上容易过拟合？

CNN中依赖卷积操作提取特征，其中有局部性、平移不变性等先验知识，而ViT中仅引入了非常少的图像先验知识，完全依靠模型学习图像patch之间的关系。

自注意力机制在图像处理中可能面临哪些计算效率问题？ViT如何通过patch划分缓解这一问题？

如果将图像中的每个像素看作token输入到模型中，QKV的计算时会面临大矩阵乘法问题，导致计算效率降低，而ViT通过划分patch、将每个patch作为token，减少了token的序列长度，从而缓解了上面的大矩阵乘法问题。

当输入图像分辨率与预训练模型不匹配时，ViT需要如何调整？试解释位置编码插值的实现逻辑

在原始的预训练得到的位置编码的基础上，根据图像位置的关系进行2D插值。

从ViT的实验结果来看，为什么它在ImageNet-21k等大规模数据集上的表现优于CNN？这种优势是否能迁移到小规模数据集？

ViT通过全局自注意力机制，可以在不引入先验知识的情况下，学习到图像的通用特征，因此在大规模数据上性能优于CNN；同时如果使用少样本微调，ViT的性能也好过CNN。

在工业场景（如医学影像分析或自动驾驶）中部署ViT时，可能面临哪些实际挑战？列举三种优化策略并说明原理

开放性问题，留给读者思考\^_\^

代码实现

这里我们自顶向下看一下模型的实现代码，我选择了一个开源的pytorch实现进行说明。

class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
        super().__init__()
        image_height, image_width = pair(image_size)
        patch_height, patch_width = pair(patch_size)
	# 确保图像可以被正确划分为多个patch
        assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'
	# 计算patch的数量
        num_patches = (image_height // patch_height) * (image_width // patch_width)
	# 对patch进行展平后得到的数据维度（注意考虑了通道）
        patch_dim = channels * patch_height * patch_width
        assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
	# 初始化patch embedding层，首先打patch，接着进行层归一化和线性层（处理为model hidden dims），再经过一个层归一化
        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width),
            nn.LayerNorm(patch_dim),
            nn.Linear(patch_dim, dim),
            nn.LayerNorm(dim),
        )
	# 位置编码是可学习的参数，注意num_patches+1代表在patches中拼接了class token
        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
	# class token，可学习参数，维度和model hidden dims相同
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
        self.dropout = nn.Dropout(emb_dropout)
	# transformer中的编码器层
        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()			# 残差层

        self.mlp_head = nn.Linear(dim, num_classes)	# 分类头

    def forward(self, img):
        x = self.to_patch_embedding(img)		# 首先对图像进行patch
        b, n, _ = x.shape				# 得到batch_size, nums_patches

        cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b = b)	# batch_size个位置编码
        x = torch.cat((cls_tokens, x), dim=1)				# class token和图像patch进行拼接
        x += self.pos_embedding[:, :(n + 1)]				# 与位置编码进行element-wise add
        x = self.dropout(x)

        x = self.transformer(x)						# 经过编码器层

        x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]

        x = self.to_latent(x)
        return self.mlp_head(x)				# 得到最终的分类结果

接着来看一下这个实现版本中的tranfromer结构。

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout),		# 多头自注意力
                FeedForward(dim, mlp_dim, dropout = dropout)					# 前向计算层
            ]))

    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x	# 多头注意力+残差
            x = ff(x) + x	# 前向计算+残差

        return self.norm(x)	# 最后进行层归一化

其中的多头注意力见下：

class Attention(nn.Module):
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.norm = nn.LayerNorm(dim)

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        x = self.norm(x)

        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)	# 将[batch_size, lens, (heads * dim/heads)] -> [batch_size, heads, lens, heads*dim]

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale	# 计算注意力分数

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)					# 得到注意力的结果
        out = rearrange(out, 'b h n d -> b n (h d)')				# 恢复尺寸
        return self.to_out(out)

另外MLP层的实现比较简单，因此这里不再做赘述。

PREVIOUS【论文阅读】Transformer-Attention is all you need（简介+代码）

NEXT【论文阅读】MAE：Masked Auto-Encoder（简介+代码+面经）