最近在看自己小方向的两篇基础模型的论文,都是在MAE(Masked AutoEncoder)上开展的工作,所以沿着MAE -> ViT -> Transformer的路线又回顾了一下这几个经典的工作,也对之前学习中模糊的地方进行了重新思考,所以打算把这几个经典的工作都写一下博客。和之前的论文阅读系列不同,我会修改一下论文的介绍顺序(参考李沐老师论文阅读方法,顺序为Abstract-Introdution-Conclusion-Background-Method-Results),尝试深入浅出梳理论文的思路,并加入代码介绍的部分。下面就一起来看下这篇DL领域不可不读的论文,如果有误或有问题,欢迎交流~
前言
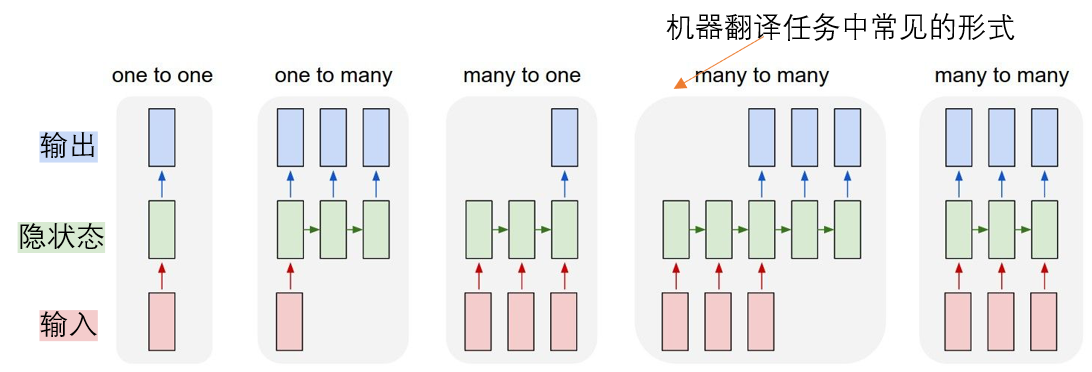
这篇工作是Google在2017年发布的,其首次完全利用自注意力方法进行语言翻译任务(抛弃了RNN和CNN),在语言翻译任务上取得了SOTA效果,并且和其他模型相比训练成本大大降低。简单回顾一下传统RNN用作NLP任务的局限,下面是常见的几种RNN形式,可以看到RNN均会维护一个隐状态,这个隐状态会包含过去所有的历史信息从而用于预测未来的任务,在最初的时序任务中,隐状态这一概念可以使得模型不必引入马尔可夫假设的约束(即不必考虑预测当前时刻时应该考虑过去哪些输入信息,隐状态已经包含了历史所有信息),从而使得模型更加灵活。但是用于机器翻译等任务时,隐状态会存在以下三个严重的问题:
- 对单一序列来说,计算是串行的,即必须输入全部的数据之后模型才可以根据隐状态进行输出,导致训练效率很低;
- 当序列长度过长时,显存限制导致batch size只能取一个很小的值,那么又会大大降低训练效率;
- RNN对序列中两个较远位置的依赖关系的捕捉能力有限。
针对这些问题,有许多方法都是在RNN上添加了一些小trick来尝试提高训练效率,但是RNN的串行计算的本质没有改变,所以性能的提升也非常有限;同时当时已经出现了一些注意力机制,可以直接对任意位置数据的关系进行建模,受到这里的启发,作者就在思考能否抛弃RNN的框架,利用注意力思想直接对所有位置的数据进行两两计算,从而得到序列的建模关系,这样的话可以抛弃串行计算的框架,并且序列元素两两计算可以用矩阵乘法实现,而GPU底层对其进行了非常多的加速操作,这样就可以将过去串行计算的策略转化为并行计算,从而提高训练策略。事实也证明Transfromer模型的高效性和有效性,不仅直接影响了NLP领域后续的工作(Bert、GPT系列开始百花齐放),也为CV领域提供了一种可参考的训练范式(之后我们会看一下ViT这篇论文,里面就提到了cv任务中注意力可能优于卷积操作)。
另外考虑到可能有对语言翻译任务不太熟悉的朋友(其实我也没有自己做过类似的任务orz),下面会简单说明一下语言翻译任务的一些数据预处理工作(注意,下面的解释只是为了简单理解Transformer的数据输入,真实的翻译任务中涉及复杂的分词方法等等预处理工作)。
语言翻译任务中,由于网络只能处理数值数据,因此会对原始句子进行分词、词汇表、embedding操作再输入网络。例如翻译时”I love Nankai University”可切分为”['<BOS>','I','love','Nankai','University','<EOS>'“,接着将每个分词根据词汇表找到对应的数字索引,再根据索引输入embedding层,就可得到这个分词的数字表示(embedding层是可学习的),之后就可以自然地输入网络处理,例如如果语料库中的句长为len(这是因为考虑到网络计算的尺寸,会设置一个固定的句长len便于网络计算,当实际句长小于len时会在对应位置补0并且记录实际的有效长度valid_len),那么输入编码器的数据尺寸可以记作 [batch_size, len, embedding_dims],这就是文本输入网络前的简单预处理。
在下面的介绍中我会努力尝试把重点放在Transformer实现高效并行的原理部分^_^
摘要
当年主流的序列翻译任务都是基于encoder-decoder架构的的RNN或CNN,表现最好的是结合了encoder-decoer和注意力机制的模型。作者提出了一个新的简单的网络结构——Transformer(真的简单吗?),仅使用注意力机制,完全省去了RNN和CNN。在两个语言翻译竞赛任务中均取得了当年的SOTA结果,另外在其中一个竞赛中仅使用8块GPU训练了3.5天,训练开销相较其他方法大大降低。
引言
RNN、LSTM、门控RNN在过去的序列建模、翻译任务上是SOTA模型的范式,目前的主流工作还是围绕在优化这些模型中。但是RNN的最严重的问题在于其串行计算的结构,必须依赖上一时刻的隐状态才能计算当前时刻的预测,这使得难以并行训练,且句子过长时因为内存限制导致batch_size变小又会降低训练效率。有些方法使用tricks尝试提升训练效率,但RNN串行计算的本质没有改变,所以效果很有限。
当时的很多任务中已经验证了注意力机制的有效性,它可以不受距离约束、直接建模序列中任意位置元素的依赖关系,但是过去的方法中只是将和RNN结合使用。
这篇工作中作者提出Transformer,摒弃了RNN结构,而是完全使用注意力机制建模输入和输出的依赖关系,真正意义上允许翻译任务实现并行化训练,并且在竞赛中取得了当年的SOTA。
总结
Transformer是首个完全依赖注意力的序列翻译模型,将encoder-decoder中的RNN层替换为多头自注意力模块。对于翻译任务来说,Transformer训练速度比CNN和RNN更快,且在“WMT 2014英语-德语”和“WMT 2014 英语-法语”两个竞赛中均取得了当年的SOTA。作者对未来注意力模型在其他任务上的应用非常感兴趣(8年后的我想说,Transformer真的做到了!),计划扩展到其他任务中,例如图像、音频和视频,同时会考虑推理阶段减少解码器的顺序生成依赖。
模型结构
这里我尝试用自底向上的逻辑梳理其中的结构,希望能给读者更清晰直观的理解。
多头自注意力
首先简单介绍一下注意力的概念,我的朴素理解是“注意力 = 全局信息查询 + 加权求和”,注意力的计算中包含3部分:查询Query、键Key、值Value,例如序列预测任务(根据x预测y,相当于建模其中的函数关系),给定一些训练数据train_x、train_y和需要预测的pred_x,最朴素的思想其实是看train_x中是否有pred_x,如果存在直接取出对应的train_y就是答案,但实际上预测任务是未知的,那么参考刚刚的思路我们可以尝试找到和pred_x最相似的train_x’,那么真实的y应该和train_y’也很相似,不过考虑到噪声我们可以和所有的train_x计算相似度(全局信息查询)、根据相似度再和train_y进行加权计算,这就是注意力的核心思想。
注意力思想中最重要的部分就是相似度的度量,最常见的是加性注意力和点乘注意力,其简洁的计算形式分别见下:
\[\begin{equation} a(q,k) = tanh(W_qq+W_kk) \end{equation}\] \[\begin{equation} a(q,k) = q^Tk \end{equation}\]两种注意力的效果很相近,且考虑到GPU矩阵计算的高效性,论文中作者选择使用缩放点积注意力:
\[\begin{equation} Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \end{equation}\]注意到这里添加了缩放项,是因为如果序列长度过长导致QK计算数值过大、从而能导致sodtmax的梯度变小、优化速度变慢,因此作者添加了缩放项:key维度开根号,来抵消这种影响。
而自注意力是指查询Q、键K、值V来自同一输入,在翻译任务中就是将输入的序列同时作为Q、K、V,来学习每个单词之间的注意力关系。
到这里我们可以看到Transformer实现并行的原因:用矩阵乘法的注意力取代串行的RNN,来建模序列元素之间的依赖性,矩阵乘法本身是GPU擅长的,并且还可以进行相当多的加速操作,因此这是实现并行的一个重要原因。
作者在此基础上又添加了一个可进一步提高并行性、多视角捕捉依赖关系的模块:多头自注意力,作者设计了多个头来学习不同的特定关系(例如长距离和短距离),见下图。
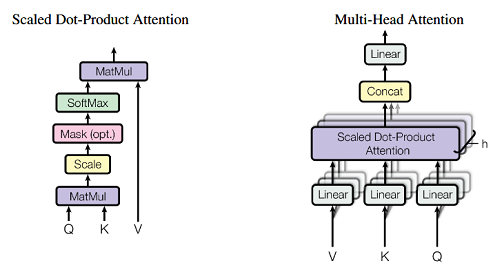
自注意力的计算流程可写作:
Q: [batch_size, nums_query, hiddens]
K: [batch_size, nums_kv, hiddens]
V: [batch_size, nums_kv, hiddens]
计算注意力权重:[batch_size, nums_query, hiddens] * [batch_size, hiddens, nums_kv] -> [batch_size, nums_query, nums_kv]
加权求和:[batch_size, nums_query, nums_kv] * [batch_size, nums_kv, hiddens] -> [batch_size, nums_query, hiddens]
在添加了多头机制之后,计算流程可以写作:
Q: [batch_size*heads, nums_query, hiddens/heads]
K: [batch_size*heads, nums_kv, hiddens/heads]
V: [batch_size*heads, nums_kv, hiddens/heads]
计算注意力权重:[batch_size*heads, nums_query, hiddens/heads] * [batch_size*heads, hiddens/heads, nums_kv] -> [batch_size*heads, nums_query, nums_kv]
加权求和:[batch_size*heads, nums_query, nums_kv] * [batch_size*heads, nums_kv, hiddens/heads] -> [batch_size*heads, nums_query, hiddens/head]
reshape操作:[batch_size, nums_query, hiddens]
在上面计算中可以看到每个头的注意力计算是独立的,因此相当于显式区分了不同注意力关系的计算过程,同时batch_size尺寸更大(变成了batch_size*heads),那么就可以进一步提高并行度。
前馈网络层
上面的多头注意力计算中只是进行矩阵乘法的计算(本质是线性操作的堆叠),关注的是全局信息,为了引入非线性表达能力、加强模块的特征提取能力,作者在多头注意力之后添加了2层全连接前馈网络,计算流程为:
\[\begin{equation} FFN(x) = max(0,xW_1+b_1)W_2+b_2 \end{equation}\]其中两个线性层分别进行升维、降维操作,可以同时捕获细粒度特征、保留核心语义特征,同时两层之间的relu激活函数引入非线性,这样就可以弥补多头注意力中只有线性计算的问题。
残差连接和层归一化
论文中作者借鉴了resnet的残差连接思想,在多头注意力和前馈网络层之间都引入了残差连接,同时添加了层归一化操作减少层和层之间数据分布的差异,从而加快收敛速度,计算过程可表示为(注意先进行残差连接、再进行层归一化):
\[\begin{equation} LayerNorm(x+Sublayer(x)) \end{equation}\]位置编码
RNN中通过串行计算隐状态来隐式加入了位置信息,但是在上面讨论的注意力机制中,缺少了位置信息的表示,为了解决这一问题,作者设计了比较简单的位置编码层,使用正余弦函数计算位置编码,并且和原始embedding数据直接进行相加操作,位置 pos处的计算公式见下,注意为了可以和原始embedding进行元素级相加,需要保证位置编码的维度和模型维度相同。
(另外补充一点,作者也尝试了将位置编码设置为可学习的参数,但二者的效果很接近,由于正余弦计算很简单不需额外学习参数,因此作者选择了这种方式)
至此Transformer模型中的重要模块均已介绍,下面来看一下模型整体框架。
模型框架
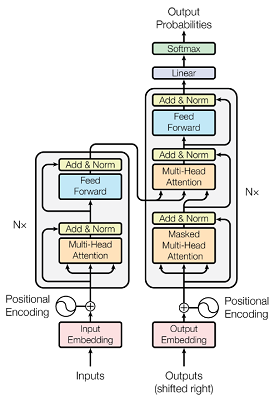
首先对模型输入进行embedding映射到数值空间,接着添加位置编码信息,模型的输入inputs是指原句子,outputs指目标句子(这里要注意的是训练阶段和推理阶段的outputs不同,训练时输入的是对应位置标签,而推理阶段输入的是前一时刻解码器的输出,两个阶段均会生成下一位置的预测概率)。
编码器比较简单,堆叠了多个解码器块,其中包括多头注意力、残差连接和层归一化、线性层,最终输出从原始句子中提取到的注意力特征。
解码器稍微复杂一些,在训练阶段,目标句子经过embedding和位置编码之后输入解码器,首先经过masked多头注意力模块(这里的masked含义是:模型预测当前位置时看不到当前位置的真实标签,只能根据过去已知的数据预测,所以对当前位置和之后的所有元素进行mask遮挡),计算目标语句的注意力之后,进入“编码器-解码器注意力”,这里的key和value均来自编码器的输出,而query来自上一个多头注意力层,参考的是seq2seq任务中的编码器解码器结构(类似第一张图中最右侧的”many-to-many”)。接着经过线性层进一步提取特征,最终多个解码器模块堆叠后的结果输入线性层和softmax激活层得到当前位置的预测概率。
以上就是模型的全部介绍,思路还是比较简单清晰的,不过具体实现时有很多细节需要注意,下面一起来看一下代码实现,我选择的是github上的一个pytorch版本实现。
代码实现
下面按照自顶向下的顺序看一下代码实现。
首先编码器的实现见下:
class Encoder(nn.Module):
''' A encoder model with self attention mechanism. '''
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200, scale_emb=False):
super().__init__()
# 编码层,使用torch.nn中的Embedding层,前两个参数分别为词表长度、嵌入维度
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
# 位置编码
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
# 多个编码层堆叠
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
# 层归一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
self.scale_emb = scale_emb
self.d_model = d_model
def forward(self, src_seq, src_mask, return_attns=False):
enc_slf_attn_list = []
# 预处理:embedding + 层归一化
enc_output = self.src_word_emb(src_seq)
if self.scale_emb:
enc_output *= self.d_model ** 0.5
enc_output = self.dropout(self.position_enc(enc_output))
enc_output = self.layer_norm(enc_output)
# 通过多个编码层
for enc_layer in self.layer_stack:
enc_output, enc_slf_attn = enc_layer(enc_output, slf_attn_mask=src_mask)
enc_slf_attn_list += [enc_slf_attn] if return_attns else []
if return_attns:
return enc_output, enc_slf_attn_list
return enc_output,
embedding使用torch.nn中提供的Embedding实现,前两个参数分别为词表大小、嵌入维度数。其中需要注意的是每个batch中不同序列的长度可能不同,因此需要为短序列填充值(例如 <POS> ),将序列调整到一致的尺寸,但是embedding参数更新时应当忽略这些填充的数据,所以需要设置 padding_idx来标记,之后如果序列中出现这个值,输出全0且不会参与梯度更新。
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
位置编码层的具体实现见下
class PositionalEncoding(nn.Module):
def __init__(self, d_hid, n_position=200):
super(PositionalEncoding, self).__init__()
# Not a parameter
self.register_buffer('pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))
def _get_sinusoid_encoding_table(self, n_position, d_hid):
''' Sinusoid position encoding table '''
# TODO: make it with torch instead of numpy
# sin和cos函数的输入
def get_position_angle_vec(position):
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
# 依次得到每个位置元素的sin和cos函数的输入
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
# 计算sin和cos
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) # dim 2i
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) # dim 2i+1
return torch.FloatTensor(sinusoid_table).unsqueeze(0)
def forward(self, x):
# 直接和输入进行element-wise相加
return x + self.pos_table[:, :x.size(1)].clone().detach()
接下来是编码器层的实现:
class EncoderLayer(nn.Module):
''' Compose with two layers '''
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(EncoderLayer, self).__init__()
# 多头注意力层
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
# 前馈网络
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(self, enc_input, slf_attn_mask=None):
# 多头注意力计算得到注意力输出和注意力分数
enc_output, enc_slf_attn = self.slf_attn(enc_input, enc_input, enc_input, mask=slf_attn_mask)
# 输入线性层前向计算
enc_output = self.pos_ffn(enc_output)
# 返回计算结果、注意力分数
return enc_output, enc_slf_attn
其中多头注意力的实现为:
class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head # 头的个数
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False) # 线性层处理QKV的输入
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
self.fc = nn.Linear(n_head * d_v, d_model, bias=False) # 线性输出层
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5) # 缩放点积注意力
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1) # batch_size, 查询的个数, 键的个数, 值的个数
residual = q # 残差计算
# Pass through the pre-attention projection: b x lq x (n*dv)
# Separate different heads: 对QKV输入进行线性层计算,并且处理为多个头的输入
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# Transpose for attention dot product: b x n x lq x dv
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
# 进行缩放点积注意力计算,得到计算结果和注意力分数
q, attn = self.attention(q, k, v, mask=mask)
# Transpose to move the head dimension back: b x lq x n x dv
# Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
q = self.dropout(self.fc(q))
q += residual # 残差连接
q = self.layer_norm(q) # 层归一化
return q, attn
缩放点积的实现为:
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9)
attn = self.dropout(F.softmax(attn, dim=-1))
output = torch.matmul(attn, v)
return output, attn
然后是前馈网络层,本质是简单的两个线性层和relu激活函数,额外添加了残差连接和层归一化。
class PositionwiseFeedForward(nn.Module):
''' A two-feed-forward-layer module '''
def __init__(self, d_in, d_hid, dropout=0.1):
super().__init__()
self.w_1 = nn.Linear(d_in, d_hid) # position-wise
self.w_2 = nn.Linear(d_hid, d_in) # position-wise
self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
residual = x
x = self.w_2(F.relu(self.w_1(x)))
x = self.dropout(x)
x += residual
x = self.layer_norm(x)
return x
decoder的结构也比较类似,考虑到篇幅限制,以及之后的MAE等模型只使用了encoder结构,因此在这里不作过多介绍,感兴趣的读者可以自行阅读源码。
后记
最近发现写博客是一个很好的帮助自己加深理解的过程,之前的非局部神经网络论文笔记中,当时其实对非局部神经网络的理解很有限,导致半个月后已经没有多少印象了,究其原因还是因为当时没有对论文有深刻的理解,有种“为了写博客而写博客”的感觉,因此希望从这篇博客开始改变一下,一是要督促自己对论文要有准确的理解和任务,不能得过且过,二是希望尝试用比较通俗的方式来描述论文的核心思想,做到这两点已经不容易,除此之外我还是希望自己的博客文章和别人的有些区别,别人写过的、很多重复的内容我不愿意再写,还是希望有自己的理解和思考,未来还是要多锻炼自己的输出能力。